Planetary gear ratio calculations
This article also available in Spanish
A question that I often get is how to work out planetary gears using the
gear template generator
 Working out the tooth counts for planetary gears is actually not that complicated,
so I initially neglected to mention how to do it.
But having received the question a number of times, I'll elaborate.
Working out the tooth counts for planetary gears is actually not that complicated,
so I initially neglected to mention how to do it.
But having received the question a number of times, I'll elaborate.
For convenience, let's denote R, S, and P as the number of teeth on the gears.
| R | Number of teeth in ring gear
|
| S | Number of teeth in sun (middle) gear
|
| P | Number of teeth in planet gears
|
The first constraint for a planetary gear to work out is that all teeth have the same pitch,
or tooth spacing. This ensures that the teeth mesh.
The second constraint is:
R = 2 × P + S
That is to say, the number of teeth in the ring gear is equal to the number of teeth
in the middle sun gear plus twice the number of teeth in the planet gears.
In the gear at left, this would be 30 = 2 × 9 + 12
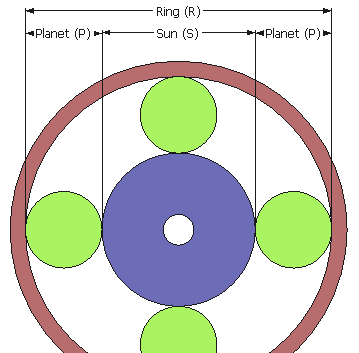 This can be made more clear by imagining "gears" that just roll (no teeth), and imagine an
even number of planet gears. From the illustration at left, you can see that the diameters
of the sun gear, plus two planet gears be must equal to the ring gear size.
This can be made more clear by imagining "gears" that just roll (no teeth), and imagine an
even number of planet gears. From the illustration at left, you can see that the diameters
of the sun gear, plus two planet gears be must equal to the ring gear size.
Now imagine we take out one of the green planet wheels, and rearrange the remaining ones
to be evenly spaced. Still the same size gear.
Now imagine the wheels have teeth. The teeth would stick out beyond the line of the wheel
as much as they indent, so that the pitch line of the gears would be the line around
the gears. The geometry still works the same. If you go into the gear generator
and select "show pitch diameter", you can see how the pitch diameter is just a circle
that the teeth are centered over.
The pitch diameter of a gear is just the number of teeth divided by diametrical pitch
(larger values of "diametrical pitch" mean smaller teeth).
The gear generator program tends to refer to tooth spacing. Pitch diameter
can also be calculated as tooth spacing * number of teeth / (2*π),
where 2*π = 6.283
 Here's another planetary gear set. The middle arrangement is removed...
Here's another planetary gear set. The middle arrangement is removed...
 ... and here it is inserted.
... and here it is inserted.
In this case, the planet gears have 12 teeth, the sun gear has 18 and the ring gear has 42 teeth.
So, applying
R = 2×P + S
We get
42 = 2 × 12 + 18
These pictures are part of a fasincatingly complicated
planetary gear drive by Ronald Walters.
Working out planetary gear turns ratios
Working out the gear ratio of a planetary gear train can be tricky.
Let's denote the following:
| Tr | Turns of the ring gear
|
| Ts | Turns of the sun gear
|
| Ty | Turns of the planetary gear carrier (the Y shaped thing in the previous photo)
|
| R | Ring gear teeth
|
| S | Sun gear teeth
|
| P | Planet gear teeth
|
The turns ratio is as follows:
( R + S ) ×Ty = R × Tr + Ts × S
Example:
Now, usually in a planetary gear, one of the gears is held fixed. For example, if we hold
the ring gear in a fixed position, Tr will always be zero.
So we can remove those terms from the above formula, and we get:
( R + S ) × Ty = Ts × S
Now, if we drive the sun gear, we can rearrange the formula to solve for turns of the Y carrier:
So the gear ratio is
S / (R+S)
Constraints on number of teeth and planets
If you want the planetary gears to be evenly spaced, and all be engaging the next tooth
at the same time, then both your sun and your ring gear needs to be evenly
divisible by the number of planets.
If you want them to be evenly spaced, but don't need them to all be in the same phase
with respect to their teeth, then then the sum of the ring gear's teeth and the sun
gear's teeth must be evenly divisible by the number of planets. That is:
( R + S ) is evenly divides by the number of planets.
If however you are willing to space the planets unevenly, this constraint does not
apply. The angle between the planet gears about the sun gear is however still constrained by:
|
Anglep2p =
| 360| ×N | | Where N is a whole number
| |
| | R+S
| |
That is to say, the angle between planet gears is a multiple of 360/(R+S).
 Finally, here's another cool arrangement of gears, though not really a "planetary" gear set.
Finally, here's another cool arrangement of gears, though not really a "planetary" gear set.
If you place a gear inside another gear, with the internal gear having a tooth count of
half the ring gear's tooth count, any point on the pitch diameter of the inside gear will
move back and forth in a straight line.
The brass rod in this photo will move strictly left to right in the slot, while the
gear it is attached to rolls around inside the ring gear. That gear is actually attached
to a crank which keeps it rolling around the edge, although only the center part
of that crank is visible, so it doesn't really look like a crank in the photo.
Photo credits:
I used some photos that were sent to me by readers.
The first and last photos were taken by Brian Kerr.
The second and third photos were sent to me by Ronald Walters
 This can be made more clear by imagining "gears" that just roll (no teeth), and imagine an
even number of planet gears. From the illustration at left, you can see that the diameters
of the sun gear, plus two planet gears be must equal to the ring gear size.
This can be made more clear by imagining "gears" that just roll (no teeth), and imagine an
even number of planet gears. From the illustration at left, you can see that the diameters
of the sun gear, plus two planet gears be must equal to the ring gear size.
 Working out the tooth counts for planetary gears is actually not that complicated,
so I initially neglected to mention how to do it.
But having received the question a number of times, I'll elaborate.
Working out the tooth counts for planetary gears is actually not that complicated,
so I initially neglected to mention how to do it.
But having received the question a number of times, I'll elaborate.
 Here's another planetary gear set. The middle arrangement is removed...
Here's another planetary gear set. The middle arrangement is removed...
 ... and here it is inserted.
... and here it is inserted. Finally, here's another cool arrangement of gears, though not really a "planetary" gear set.
Finally, here's another cool arrangement of gears, though not really a "planetary" gear set.
 Gear template generator
Gear template generator
 How to make
How to make Working out compound
Working out compound
 Pen shaking contraption
Pen shaking contraption Making right angle gears
Making right angle gears