
 We used to live in Ontario, where natural gas heating is relatively inexpensive,
so other heating options aren't really worth considering.
We used to live in Ontario, where natural gas heating is relatively inexpensive,
so other heating options aren't really worth considering.

 We used to live in Ontario, where natural gas heating is relatively inexpensive,
so other heating options aren't really worth considering.
We used to live in Ontario, where natural gas heating is relatively inexpensive,
so other heating options aren't really worth considering.
However, having moved to New Brunswick in 2018, though we have natural gas here,
on a per-heat-generated basis, its only about 15-20% cheaper than electricity.
 This makes heat pumps a relatively good choice for heating in the winter,
and I'm seeing a lot of heat pumps installed on houses around here
these days.
This makes heat pumps a relatively good choice for heating in the winter,
and I'm seeing a lot of heat pumps installed on houses around here
these days.
But how much more efficient are these than straight-up electric heating? I figured it would be good to experiment, and I realized, we already have a a similar heat pump in our refrigerator, so why not test that?

 I bought some TP-link HS110 smart plugs, which can do energy monitoring, and are
relatively easy to control and monitor using simple python scripts from a PC
(no "cloud" stuff required). I can use this to monitor how much energy the
fridge uses. I also put some DHT22 temperature sensors, hooked up to
a Raspberry Pi computer, inside the fridge and freezer to monitor the temperature during
the experiment. The Raspberry Pi computer records temperature, humidity and power
consumption every minute.
I bought some TP-link HS110 smart plugs, which can do energy monitoring, and are
relatively easy to control and monitor using simple python scripts from a PC
(no "cloud" stuff required). I can use this to monitor how much energy the
fridge uses. I also put some DHT22 temperature sensors, hooked up to
a Raspberry Pi computer, inside the fridge and freezer to monitor the temperature during
the experiment. The Raspberry Pi computer records temperature, humidity and power
consumption every minute.
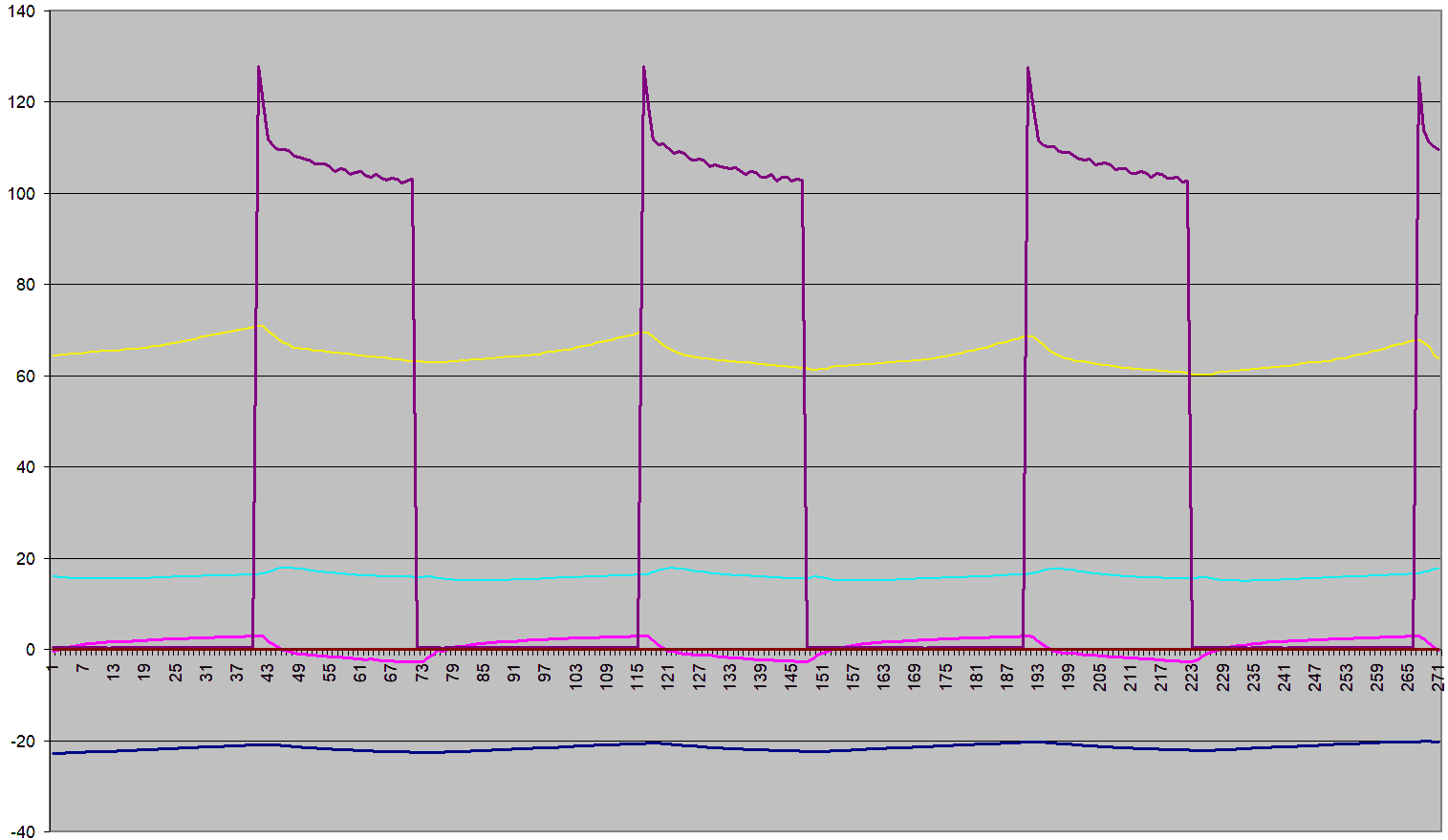 At left, a steady state graph of the refrigerator running.
At left, a steady state graph of the refrigerator running.
Graph Legend:
Dark Purple: Power consumption (Watts)
Yellow: Relative humidity, freezer (%)
Cyan: Relative humidity, fridge (%)
Purple: Fridge temperature (°C)
Blue: Freezer temperature (°C)
Time is in minutes.
The dark purple line shows the fridge running with a 42% duty cycle. While running, it draws over 100 watts, but the average power over time was only 45 watts.
 The next experiment was to put a 60-watt incandescent light bulb inside the fridge.
This bulb is also connected to a TP-Link HS110 smart plug to monitor the
actual power draw of the bulb.
The next experiment was to put a 60-watt incandescent light bulb inside the fridge.
This bulb is also connected to a TP-Link HS110 smart plug to monitor the
actual power draw of the bulb.
The goal was to see how much more power the fridge would need to pump out the heat that the 60-watt incandescent bulb adds.
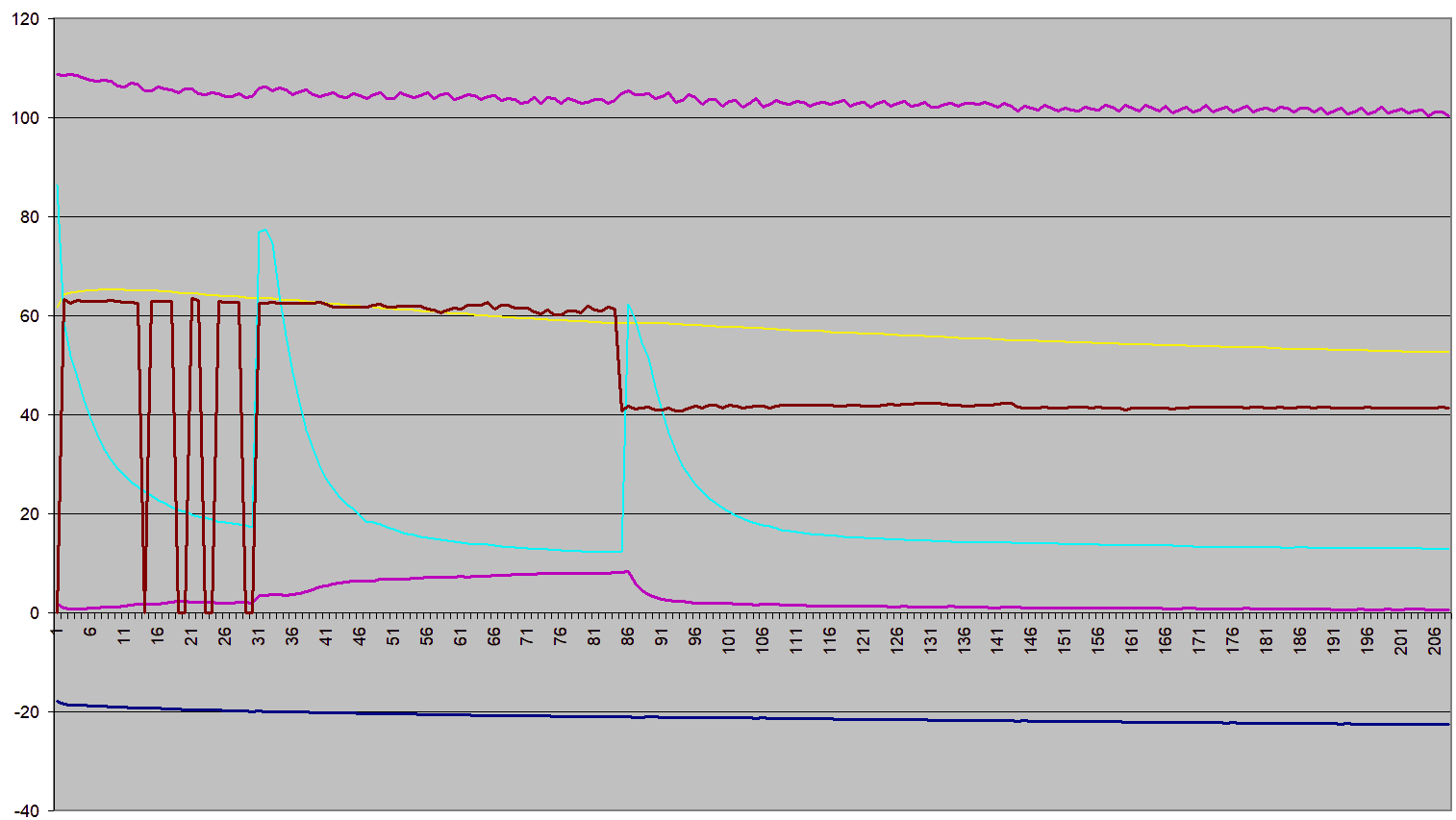 Results from the 60-watt bulb run.
Results from the 60-watt bulb run.
The brown line shows the power to the light bulb. This line zigzags up and down
at first because I had an intermittent connection with the bulb. I opened the
fridge at about minute 32 on this graph to screw the bulb in tighter. This led to
extra air getting into the fridge, which was more humid, so the relative humidity
(yellow) spiked on opening the fridge. The temperature (purple) also rose a little from
opening the fridge.
Over the next 55 minutes, I saw the temperature in the fridge slowly creep up, while the fridge's compressor ran constantly (dark purple line shows the fridge's power draw always over 100 watts)
So 60 watts was more heat than the fridge's compressor could keep up with. So I opened the fridge again and swapped it for a 40-watt bulb at about minute 86. After that, the temperature dropped to just a few degrees, but the compressor never shut off.
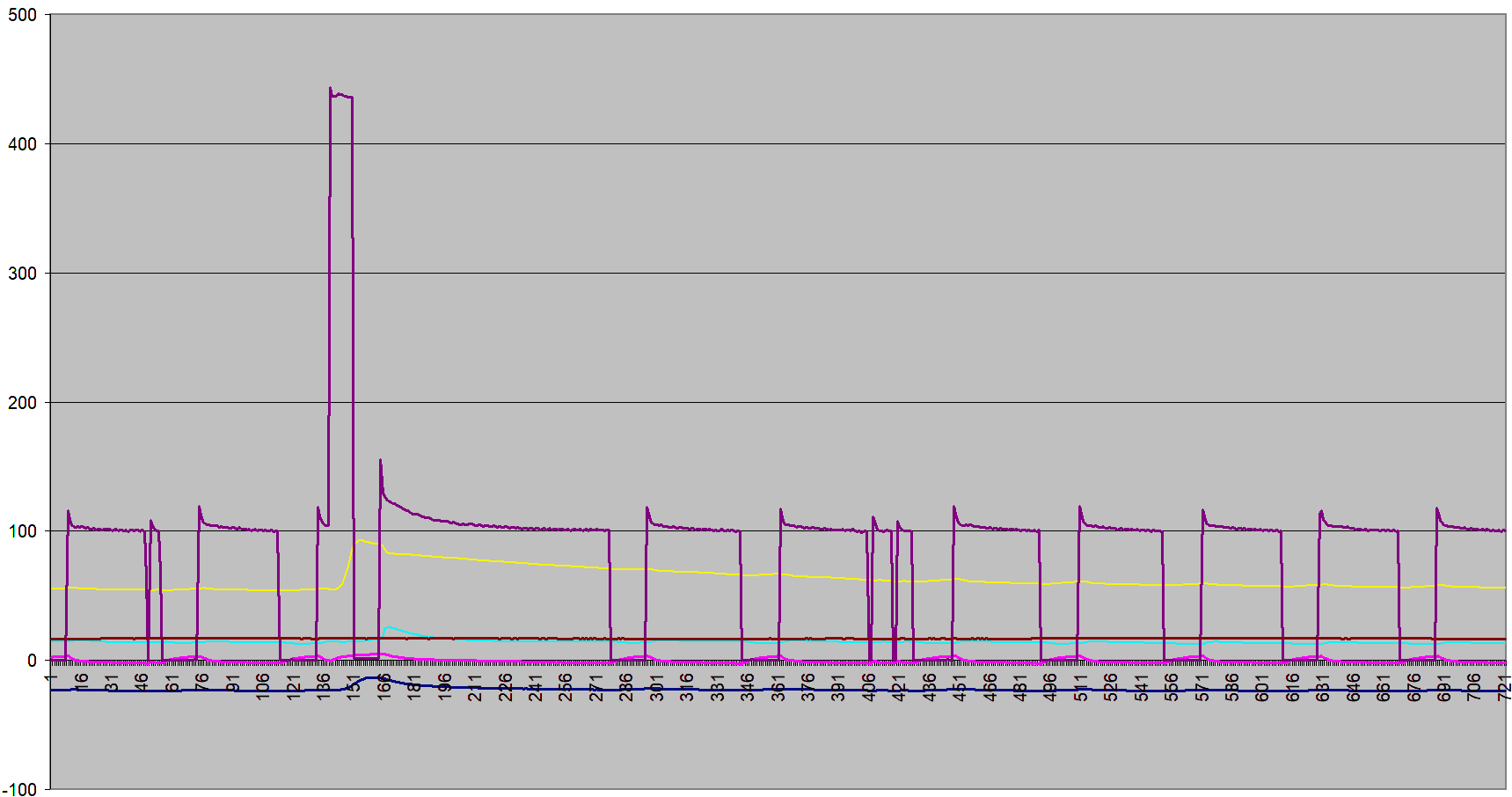 I wanted my comparison to be with the fridge running in steady state where
the compressor still cycles on and off, so I swapped the 40-watt bulb for
a 17-watt appliance bulb.
I wanted my comparison to be with the fridge running in steady state where
the compressor still cycles on and off, so I swapped the 40-watt bulb for
a 17-watt appliance bulb.
But shortly after that, the fridge used over 400 watts for about 15 minutes. Note the different scale on the graph at left. The 400-watt period was a fridge defrost cycle. Whenever air is cooled down, moisture may condense out of the air. If the air is cooled down to below freezing, this condensation turns into sublimination directly into ice, causing ice buildup on the cooling elements. Periodic heating of the cooling elements is required to melt this ice off, or it eventually clogs the cooling element.
After the defrost cycle, the compressor needs to run an extra-long cycle to cool things down again.
 So I waited until the fridge reached steady state some time after that.
So I waited until the fridge reached steady state some time after that.
With the bulb adding 16.9 watts of heat to the fridge, the compressor duty cycle was 69%. The compressor's power draw while running was about the same as before, but with the larger duty cycle, the fridge's average power consumption was now 71 watts.
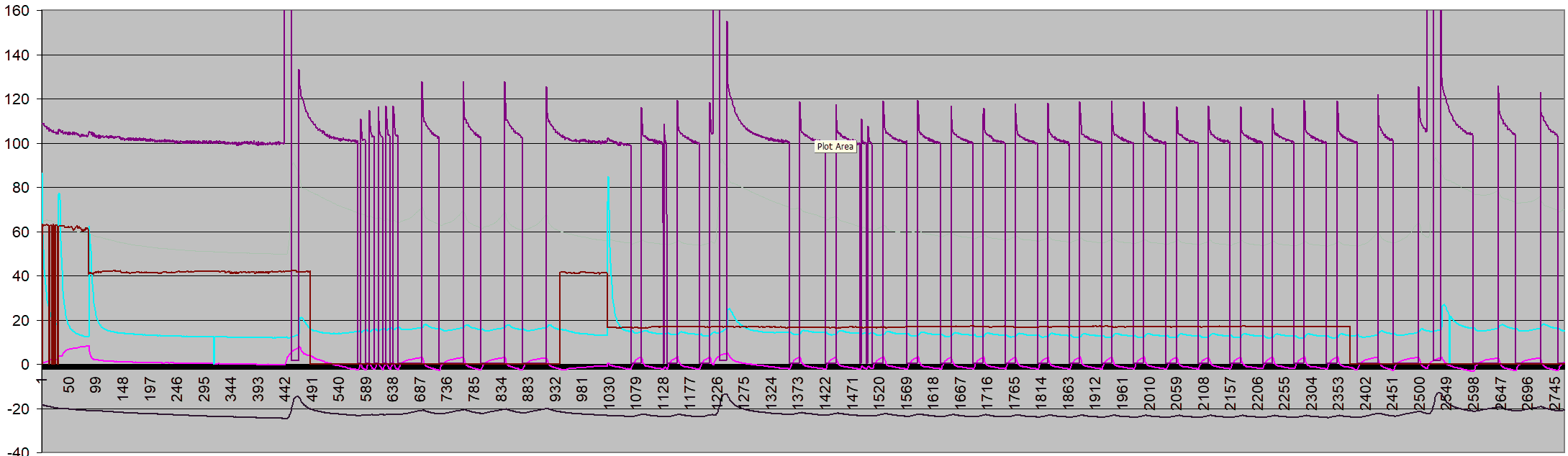 At left, a chart showing power usage for the duration of my experiments
(all previous graphs are segments of this graph)
At left, a chart showing power usage for the duration of my experiments
(all previous graphs are segments of this graph)
You can download my spreadsheet: fridge.zip
The extra 16.9 watts from the light bulb increased the fridge's duty cycle from 42% to 69%, and increased the fridge's average power consumption by 25.58 watts. This means that every extra watt the fridge used was able to pump out 0.662 watts of heat from the fridge.
A bit disappointing. I thought the fridge's heat pump would be able to pump out at least a watt of heat for each watt it used.
But the fridge is working under challenging conditions for a heat pump, in that it cools the freezer to -20°C (-4°F). House heating heat pumps don't work that well when they need to get heat from outside air that is that cold.
But even if the fridge's heat pump only extracts 0.66 watts from the cold side for each watt of electricity, the total heat into the room is 1 + 0.66, as all the electricity consumed also turns into heat in the room, so imagine instead of cooling the inside of the fridge, it was cooling the outside, the coefficient of performance would be 1.66, or about 1.66 watts of heating for every watt of electricity consumed.
But heating heat pumps are at least 20 times as powerful, and there is a certain economy of scale that goes with that. So I would expect a house heating heat pump to be more efficient.
However, one thing I didn't factor in is periodic defrost cycles needed when the air temperature gets below freezing. I deliberately avoided including those in the fridge experiment, or I would have had to do much longer runs because the defrost only happens about every 24 hours. And a fridge will probably have less condensation to deal with than a heating heat pump because the air in the fridge eventually becomes very dry, whereas there is a lot more outside air with an unlimited supply of moisture.
But even so, the heat required to melt a volume of ice is only about 20% of the heat that was released when the moisture subliminated from vapour in the air into ice. And not all the heat extracted from the outside is the result of condensation, so the defrost cycles are a relatively minor factor. Nonetheless, none of the energy used for defrosting ends up in the house, so from a heating perspective, it's energy entirely wasted.
 With a heat pumping out coefficient of performance of just 0.66, and an average power draw
of 45 watts, this suggests there is about 30 watts of heat leaking into the fridge through
the walls at all times. Taking the fridge wall area and fridge and freezer temperature difference
into account, this suggests the insulation of the fridge walls is about R20, which seems
kind of high for a fridge, so I'm not sure if this is correct.
With a heat pumping out coefficient of performance of just 0.66, and an average power draw
of 45 watts, this suggests there is about 30 watts of heat leaking into the fridge through
the walls at all times. Taking the fridge wall area and fridge and freezer temperature difference
into account, this suggests the insulation of the fridge walls is about R20, which seems
kind of high for a fridge, so I'm not sure if this is correct.
I did another experiment, covering the fridge with several warm duvets. This reduced the fridge's steady state power consumption by only 10%, so it does suggest that the fridge's insulation is quite good.
 Looking at the specs on this heat pump at left (click image to enlarge),
we can calculate:
Looking at the specs on this heat pump at left (click image to enlarge),
we can calculate:
208 Volts * 11.9 Amperes = 2475 watts
1600 BTU/HR = 4689 watts
4689 watts out/2475 watts in = 1.89
So by those specs, the heat pump has a coefficient of performance of 1.89, or it will provide 1.89 watts of heat for every watt it uses. But performance is very much a function of inside and outside temperature, and I don't know what outside temperature that assumes.
But searching for "Fujitsu heat pump coefficient of performance" on google brings up this link:
[PDF] Laboratory Test Report for Fujitsu 12RLS and Mitsubishi ... - NREL
Some interesting numbers there. The relative loss due to defrost cycles is indeed
relatively small, and a COP of around 2 is achievable even if it's around -20°c outside.
But is a heat pump really worth it? If you already have electric heat, it's a high initial cost
that will take years to pay for itself. In the mean time, electric heat is silent, reliable,
and exactly where you need it, and there's no risk of it breaking down. I think we should get a
heat pump for our house eventually, but factoring in capital costs, lifetime, and other issues,
it's not a huge win - unless you also use the heat pump for cooling your house. By my estimates,
we'd be saving at most $1000 per year, for a system that might cost us $10,000. If that system
were to last 20 years without any additional expenses, the savings would still be relatively small.
I think the key is that a heat pump also provides air conditioning, and there were about 5-10 days this summer where air conditioning would have been nice. Which is not to say there weren't more than 10 hot days, just that the nights here are relatively cool, and opening the windows at night was enough to keep the house cool most of the time.
 Does dusting out a fridge make a difference (video only)
Does dusting out a fridge make a difference (video only) Infrared heater: How warm does it feel (video only)
Infrared heater: How warm does it feel (video only)