Spacing spindles evenly
A problem often encountered in woodworking is to space spindles, or slats or anything
out evenly so that there are even gaps. This problem is pretty straightforward if
the width of whatever needs to be spaced doesn't need to be taken into account. But
when spacing boards, slats or spindles, and the gaps should all be the same size,
(including gaps at the end) it gets a little bit more tricky.
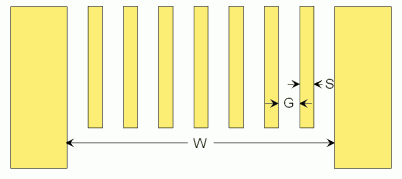 Suppose we have 7 spindles, that we want to space with even gaps, including the gaps
on either end, across width W. If we were to space the centers in the space, it would
not be too bad, but the gap 'G' on either end would be narrower than the gaps between the
spindles.
Suppose we have 7 spindles, that we want to space with even gaps, including the gaps
on either end, across width W. If we were to space the centers in the space, it would
not be too bad, but the gap 'G' on either end would be narrower than the gaps between the
spindles.
The proper thing to do in this case would be to take the total width W, and remove 7
times the width of the spindle 'S', and divide that into 8 (number of gaps, which
is one greater than the number of spindles) to get the size of the gap.
But then measuring all this out gets complicated.
The easy method:
 Simply add the width of one spindle to the width 'W'. You can do this by just placing
an extra spindle next to the gap and measuring it to that. Now we have the width
that 8 spindles and 8 gaps would take up.
So we can just divide that by 8, to get the width of a spindle plus the
width of a gap. The key is to divide this width plus a spindle width by one more than the
number of spindles.
Simply add the width of one spindle to the width 'W'. You can do this by just placing
an extra spindle next to the gap and measuring it to that. Now we have the width
that 8 spindles and 8 gaps would take up.
So we can just divide that by 8, to get the width of a spindle plus the
width of a gap. The key is to divide this width plus a spindle width by one more than the
number of spindles.
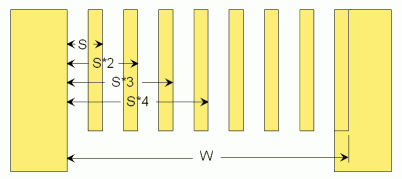
 The next thing is to hook or push the tape measure against the end, and work out
all the positions with a calculator. The 'constant calculation' feature of any five
function calculator is very suited to that. Simply punch in the number from the above
calculation and push '+', then '='. The calculator will show the number plus itself,
which is the position of the second spindle (S*2). Now push '=' again, and the number
will once again be added, giving you S*3. And so on. Every time you push '=', read the
number off your calculator and, without moving your tape measure, mark that position on it.
Do this for every spindle, and you will have the right side edge of every spindle or slat.
The next thing is to hook or push the tape measure against the end, and work out
all the positions with a calculator. The 'constant calculation' feature of any five
function calculator is very suited to that. Simply punch in the number from the above
calculation and push '+', then '='. The calculator will show the number plus itself,
which is the position of the second spindle (S*2). Now push '=' again, and the number
will once again be added, giving you S*3. And so on. Every time you push '=', read the
number off your calculator and, without moving your tape measure, mark that position on it.
Do this for every spindle, and you will have the right side edge of every spindle or slat.
 Suppose we have 7 spindles, that we want to space with even gaps, including the gaps
on either end, across width W. If we were to space the centers in the space, it would
not be too bad, but the gap 'G' on either end would be narrower than the gaps between the
spindles.
Suppose we have 7 spindles, that we want to space with even gaps, including the gaps
on either end, across width W. If we were to space the centers in the space, it would
not be too bad, but the gap 'G' on either end would be narrower than the gaps between the
spindles.
 Simply add the width of one spindle to the width 'W'. You can do this by just placing
an extra spindle next to the gap and measuring it to that. Now we have the width
that 8 spindles and 8 gaps would take up.
So we can just divide that by 8, to get the width of a spindle plus the
width of a gap. The key is to divide this width plus a spindle width by one more than the
number of spindles.
Simply add the width of one spindle to the width 'W'. You can do this by just placing
an extra spindle next to the gap and measuring it to that. Now we have the width
that 8 spindles and 8 gaps would take up.
So we can just divide that by 8, to get the width of a spindle plus the
width of a gap. The key is to divide this width plus a spindle width by one more than the
number of spindles.
 The next thing is to hook or push the tape measure against the end, and work out
all the positions with a calculator. The 'constant calculation' feature of any five
function calculator is very suited to that. Simply punch in the number from the above
calculation and push '+', then '='. The calculator will show the number plus itself,
which is the position of the second spindle (S*2). Now push '=' again, and the number
will once again be added, giving you S*3. And so on. Every time you push '=', read the
number off your calculator and, without moving your tape measure, mark that position on it.
Do this for every spindle, and you will have the right side edge of every spindle or slat.
The next thing is to hook or push the tape measure against the end, and work out
all the positions with a calculator. The 'constant calculation' feature of any five
function calculator is very suited to that. Simply punch in the number from the above
calculation and push '+', then '='. The calculator will show the number plus itself,
which is the position of the second spindle (S*2). Now push '=' again, and the number
will once again be added, giving you S*3. And so on. Every time you push '=', read the
number off your calculator and, without moving your tape measure, mark that position on it.
Do this for every spindle, and you will have the right side edge of every spindle or slat.