
 Having moved into a new (old) home, in New Brunswick, where heating is expensive
on account of not having cheap natural gas, I was obsessing about insulation
and such.
Having moved into a new (old) home, in New Brunswick, where heating is expensive
on account of not having cheap natural gas, I was obsessing about insulation
and such.

 Having moved into a new (old) home, in New Brunswick, where heating is expensive
on account of not having cheap natural gas, I was obsessing about insulation
and such.
Having moved into a new (old) home, in New Brunswick, where heating is expensive
on account of not having cheap natural gas, I was obsessing about insulation
and such.
Using an infrared thermometer, I devised a way to measure the insulation R-value of the outside walls of the house.
On a cold day, when the outside temperature was -15°C, I measured the wall temperature of our bedroom at 13.3°C, and a dresser near the same wall at 14.8°C. We like to keep the bedrooms at a cool temperature.
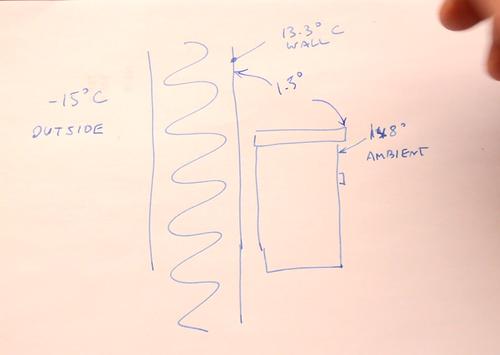 It's best to pick a surface near the outside wall, at the same height, and parallel
to it for measuring the ambient temperature, because the temperature throughout
a room can vary by a few degrees.
It's best to pick a surface near the outside wall, at the same height, and parallel
to it for measuring the ambient temperature, because the temperature throughout
a room can vary by a few degrees.
Assuming the dresser is at the room's ambient temperature, the 1.5° temperature difference is taken up by the insulation properties of the air boundary layer to the wall. This is assuming all temperatures are at steady state, and that the sun isn't shining on either side of the wall.
The effective R value of the wall surface, at a 1.5 degree temperature difference is R 0.728 (or Rsi of 0.13). R-value is measured in BTU per square foot per degree (F) heat transfer, whereas Rsi is degrees C per Watts per square meter To convert Rsi to R(imperial), Multiply Rsi by 5.8.
 Given a 28.3 degree temperature difference to the outside, and knowing that heat transfer
is temperature difference over R value, and that the amount of heat transferred through
the wall is the same as the heat transfer across the surface, we can write the equation:
Given a 28.3 degree temperature difference to the outside, and knowing that heat transfer
is temperature difference over R value, and that the amount of heat transferred through
the wall is the same as the heat transfer across the surface, we can write the equation:
| 28.3° | 1.5° | |
| ———— | = | ——— |
| Runknown | R 0.738 |
From this, we can solve for Runknown = R0.738 * 28.3° / 1.5° = 13.9
Which works out very close to the expected value because the walls of the house have 3 5/8" of fiberglass insulation between the 2x4s. But there is also 3/4" of wood sheathing on the outside, plus a 1 1/4" air gap, and 3.5" of bricks. Each of these adds a little to the insulation, which I assume accounts for the difference between the expected R12 for the fiberglass and the measured R13.9
 This all relies on being able to measure the surface temperature fairly accurately, and
these relatively cheap infrared thermometer are a limiting factor. The one at left is
one I bought quite cheaply for $20 Canadian. I found that one a bit inaccurate, especially
if the battery gets low, or the temperature of the thermometer itself varies too much.
The one at right cost $40 Canadian ordered on line and works much better.
This all relies on being able to measure the surface temperature fairly accurately, and
these relatively cheap infrared thermometer are a limiting factor. The one at left is
one I bought quite cheaply for $20 Canadian. I found that one a bit inaccurate, especially
if the battery gets low, or the temperature of the thermometer itself varies too much.
The one at right cost $40 Canadian ordered on line and works much better.
 For relative measurements, the absolute accuracy doesn't matter that much. But I found when
measuring temperatures just a degree or so apart, the thermometers didn't realize a new
measurement was being taken and just kept averaging with the previous reading. To get
around this, it's best to measure something very different in temperature between
readings, such as the surface of my hands.
For relative measurements, the absolute accuracy doesn't matter that much. But I found when
measuring temperatures just a degree or so apart, the thermometers didn't realize a new
measurement was being taken and just kept averaging with the previous reading. To get
around this, it's best to measure something very different in temperature between
readings, such as the surface of my hands.
It also helps to go back and forth and repeat the measurements a few times, just to make sure the number you have is representative. Being off by 0.2 degrees in this case would change the result by 15%.
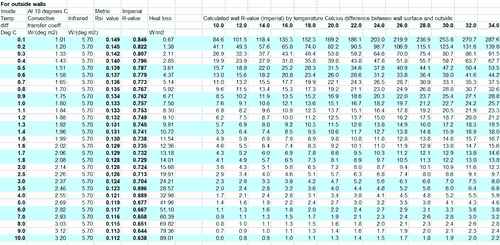 I made a spreadsheet for calculating the R-value of the boundary layer based on
temperature difference. Then, to save you some algebra, I also included columns of the
calculated wall R-value based on the temperature difference to the outside.
I made a spreadsheet for calculating the R-value of the boundary layer based on
temperature difference. Then, to save you some algebra, I also included columns of the
calculated wall R-value based on the temperature difference to the outside.
Download the Excel spreadsheet
There is also a column for heat loss, measured in watts per square meter of wall, which allows you to calculate the rate of heat loss through the walls of your house.
Please note that the version of the spreadsheet used in the video had an error in the formula for the column for heat loss (W/m2). The version here is fixed. Fortunately, that number wasn't used for the R-value calculations.
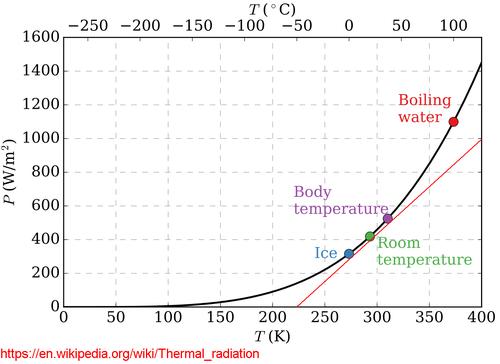 Surface heat transfer is a function of heat conducted into and carried away by
the air (convection) and thermal (infrared) radiation, the same type
of radiation that an infrared thermometer picks up.
Surface heat transfer is a function of heat conducted into and carried away by
the air (convection) and thermal (infrared) radiation, the same type
of radiation that an infrared thermometer picks up.
I looked up "thermal radiation" on Wikipedia. The slope of this graph doesn't change much between freezing and body temperature, so I drew a red line roughly parallel, and measured it's slope. The line rises by 1000 watts/m2 over a temperature range from 225 to 400°Kelvin. 1000 watts divided by (400-225) = 5.7 watts/m2°C.
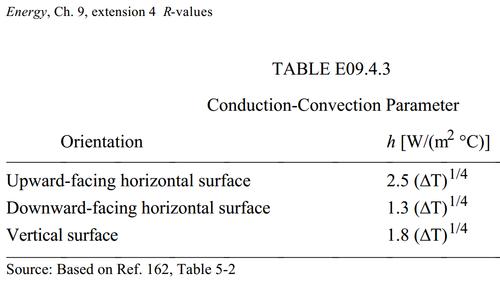 The other component of surface heat transfer is heat conduction to the air, assuming
there is no wind. Warming or cooling the air causes convection, which in turn increases
the rate of heat transfer, which means the heat transfer rate increases faster than
temperature. I used the formula for "vertical surface" at left, from
this document
and plugged that into the spreadsheet.
The other component of surface heat transfer is heat conduction to the air, assuming
there is no wind. Warming or cooling the air causes convection, which in turn increases
the rate of heat transfer, which means the heat transfer rate increases faster than
temperature. I used the formula for "vertical surface" at left, from
this document
and plugged that into the spreadsheet.
I then added the two conductances as a function of temperature and calculated the inverse of conductance to get thermal resistance, Rsi (in metric). Multiplying Rsi by 5.8 converts it to R-values for imperial units. The imperial units are useful for comparing insulation, as most insulation here (in Canada and in the US) is rated in imperial R-values. But Metric Rsi values are much more useful for calculating heat loss, unless you like to suffer and perform thermodynamics in imperial units. When I took thermodynamics, we had to learn to do it in both systems of measurements, and we not allowed to just convert to Metric, do the calculation, and convert back, because that would have been easier than calculating thermodynamics in imperial units.
Correction — Spreadsheet error, 20% off:
The "W/m2" column of my spreadsheet had an error in the formula. I fixed this
in the dowloadable spreadhseet, but couldn't change the video. The error
ended up throwing my energy calculation off by 20%. The actual savings are 20% higher.
Follow up (2021):
16 months later I experimented with monitoring when the tank turns on and off, among other things
in this video. While away for the weekend,
the heater would go 10.5 hours without turning the heater on, then turns the 800 watt element
on for about 1.25 hours to re-heat. Based on this:
1.25 / (10.5 + 1.25) * 800 watts = 85 watts average to maintain temperature.
85 watts * 24 hours = 2.04 kWh per day to maintain temperature (not counting any hot water usage).
In the above video at 1:30 I worked out that it's losing 1.66 kWh/day, but that's with the spreadsheet with the error, so adding the 20% spreadsheet error takes it to 2 kWh per day.
But the ambient in the video was 14 degrees, vs 19 degrees in July, so the power use in July should have been 10% lower. Another heat loss that I hadn't taken into account with my calculation in the video is that the pipes to the tank also lose heat, so the estimate in the video should have been on the low side. My measurements of power use included that.
That said, I didn't measure the actual power of the element, which may or may not consume exactly 800 watts. Line voltage could be anywhere from 110 to 125 volts and still be within "spec", which will change both voltage and current in a resistive element, potentially changing power usage by as much as 1.5 times. So the power usage calculation may also have inaccuracies. But I'm happy that I got it as close as I did using just an infrared thermometer and a calculator.
If you get a better insulating blanket and pay less for it and your electricity costs are higher than here the payback period could end up less than one year. So these blankets may make sense under some circumstances.
 Does dusting out a fridge make a difference (video only)
Does dusting out a fridge make a difference (video only) Mysterious water drip investigation (video only)
Mysterious water drip investigation (video only) Building an air raid siren
Building an air raid siren