 Have you ever wondered why when you strike a bell (or in this case, a bowl)
the sound usually oscillates between louder and quieter while it
rings out instead of just slowly becoming quieter? This is what this article
is about.
Have you ever wondered why when you strike a bell (or in this case, a bowl)
the sound usually oscillates between louder and quieter while it
rings out instead of just slowly becoming quieter? This is what this article
is about.
 Have you ever wondered why when you strike a bell (or in this case, a bowl)
the sound usually oscillates between louder and quieter while it
rings out instead of just slowly becoming quieter? This is what this article
is about.
Have you ever wondered why when you strike a bell (or in this case, a bowl)
the sound usually oscillates between louder and quieter while it
rings out instead of just slowly becoming quieter? This is what this article
is about.
 This phenomenon is easier to illustrate with a pendulum that can
swing in two directions.
the string is tied into a 'Y' at the top, with both ends clamped to the bar
above. If I swing the pendulum perpendicular to the bar, the length
of the pendulum is from the weight to where the strings are attached
to the bar. But if I swing it parallel to
the bar, then the effective length is from the weight to the knot that
makes a 'Y', a shorter length. Because the pendulum's period of oscillation
is in proportion to its length, the pendulum swings faster on the axis
parallel to the bar than perpendicular to it.
This phenomenon is easier to illustrate with a pendulum that can
swing in two directions.
the string is tied into a 'Y' at the top, with both ends clamped to the bar
above. If I swing the pendulum perpendicular to the bar, the length
of the pendulum is from the weight to where the strings are attached
to the bar. But if I swing it parallel to
the bar, then the effective length is from the weight to the knot that
makes a 'Y', a shorter length. Because the pendulum's period of oscillation
is in proportion to its length, the pendulum swings faster on the axis
parallel to the bar than perpendicular to it.
If I swing the pendulum diagonal to the bar, rather than tracing out a straight line, the path of the weight forms a Lissajous curve. But viewed horizontally, at an angle to the bar, it looks like the pendulum's swing increases and decreases with time. What you actually see is the sum of two sinusoidal swings of different frequencies. When they are in phase, the swing looks strong, but when they are out of phase, the only swing is towards / away from the viewer, and the swing doesn't look big.
Words don't really do this justice - I'd recommend you watch the video at the top of this article.
 The bell's sound alternating between louder and weaker is also the result
of two sine waves of slightly different frequencies which sometimes times
add up and at other times oppose, partially cancelling each other.
The bell's sound alternating between louder and weaker is also the result
of two sine waves of slightly different frequencies which sometimes times
add up and at other times oppose, partially cancelling each other.
In terms of how a bell rings at two frequencies, you can think of a bell as a cylinder. The main mode of vibration is that the cylinder alternately stretches vertically (while compressing horizontally), and swings back to stretching horizontally while compressing vertically.
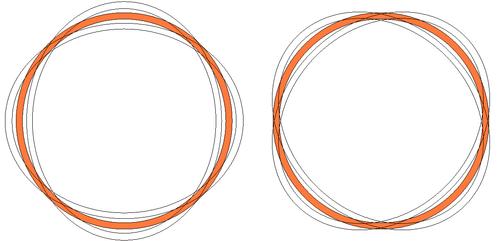 But this mode of vibration (left image at left) is independent of vibrations
at a 45-degree angle to that (right image at left). Due to imperfections, either
deliberate or accidental, these two modes of vibration are often at slightly
different frequencies.
But this mode of vibration (left image at left) is independent of vibrations
at a 45-degree angle to that (right image at left). Due to imperfections, either
deliberate or accidental, these two modes of vibration are often at slightly
different frequencies.
 This piece of pipe, when struck, will slowly get louder and quieter.
This piece of pipe, when struck, will slowly get louder and quieter.
I figured it would be a fun experiment to modify it to move the two frequencies of oscillation further apart.
 I ground two flat spots on opposite sides of the pipe. Already, this made it
sound quite different, making two notes about a semitone (6% change in pitch) apart.
I ground two flat spots on opposite sides of the pipe. Already, this made it
sound quite different, making two notes about a semitone (6% change in pitch) apart.
I ground it some more, grinding four flat spots on it corresponding to the nodes of one mode of vibration or the peaks of the other main mode of vibration.
 Striking the cylinder half way between the flat spots excites only the higher frequency
mode of vibration. I measured it at 1100 Hz, or just below C-sharp two octaves
above middle C on a piano. The guitar tuner is able to pick up the note.
Striking the cylinder half way between the flat spots excites only the higher frequency
mode of vibration. I measured it at 1100 Hz, or just below C-sharp two octaves
above middle C on a piano. The guitar tuner is able to pick up the note.
 The other mode of vibration is 864 Hz, or about a third of a semitone below
the second A above middle C. The ratio between these
is about 1.27, an interval slightly larger than 5/4 or a "major third" in terms
of music.
The other mode of vibration is 864 Hz, or about a third of a semitone below
the second A above middle C. The ratio between these
is about 1.27, an interval slightly larger than 5/4 or a "major third" in terms
of music.
 Playing the two notes the bell plays on the piano while the bell is ringing.
The sound is very similar.
Playing the two notes the bell plays on the piano while the bell is ringing.
The sound is very similar.
I should add that I wasn't trying to tune to any particular musical note or interval with my "bell", it just happened to work out that way. It's difficult to tune such a bell to hit two specific notes because any grinding done to it will affect both notes.
 But the coolest feature of this "bell" is that if I strike it so both notes sound, then spin
it, you can hear the two pitches alternate. That's because each of the two main modes of
vibration sends sound in different directions.
But the coolest feature of this "bell" is that if I strike it so both notes sound, then spin
it, you can hear the two pitches alternate. That's because each of the two main modes of
vibration sends sound in different directions.
 Gyro effect explained
Gyro effect explained The hui game. Also
The hui game. Also Building an air raid siren
Building an air raid siren